We conduct experiments on MiniF2F and ProofNet.
Recent advancements in neural theorem proving integrate large language models with tree search algorithms like Monte Carlo Tree Search (MCTS), where the language model suggests tactics and the tree search finds the complete proof path. However, many tactics proposed by the language model converge to semantically or strategically similar, reducing diversity and increasing search costs by expanding redundant proof paths. This issue exacerbates as computation scales and more tactics are explored per state. Furthermore, the trained value function suffers from false negatives, label imbalance, and domain gaps due to biased data construction. To address these challenges, we propose CARTS (diversified tactic CAlibration and bias-Resistant Tree Search), which balances tactic diversity and importance while calibrating model confidence. CARTS also introduce preference modeling and an adjustment term related to the ratio of valid tactics to improve the bias-resistance of the value function. Experimental results demonstrate that CARTS consistently outperforms previous methods achieving a pass@l rate of 49.6\% on the miniF2F-test benchmark. Further analysis confirms that CARTS improves tactic diversity and leads to a more balanced tree search.
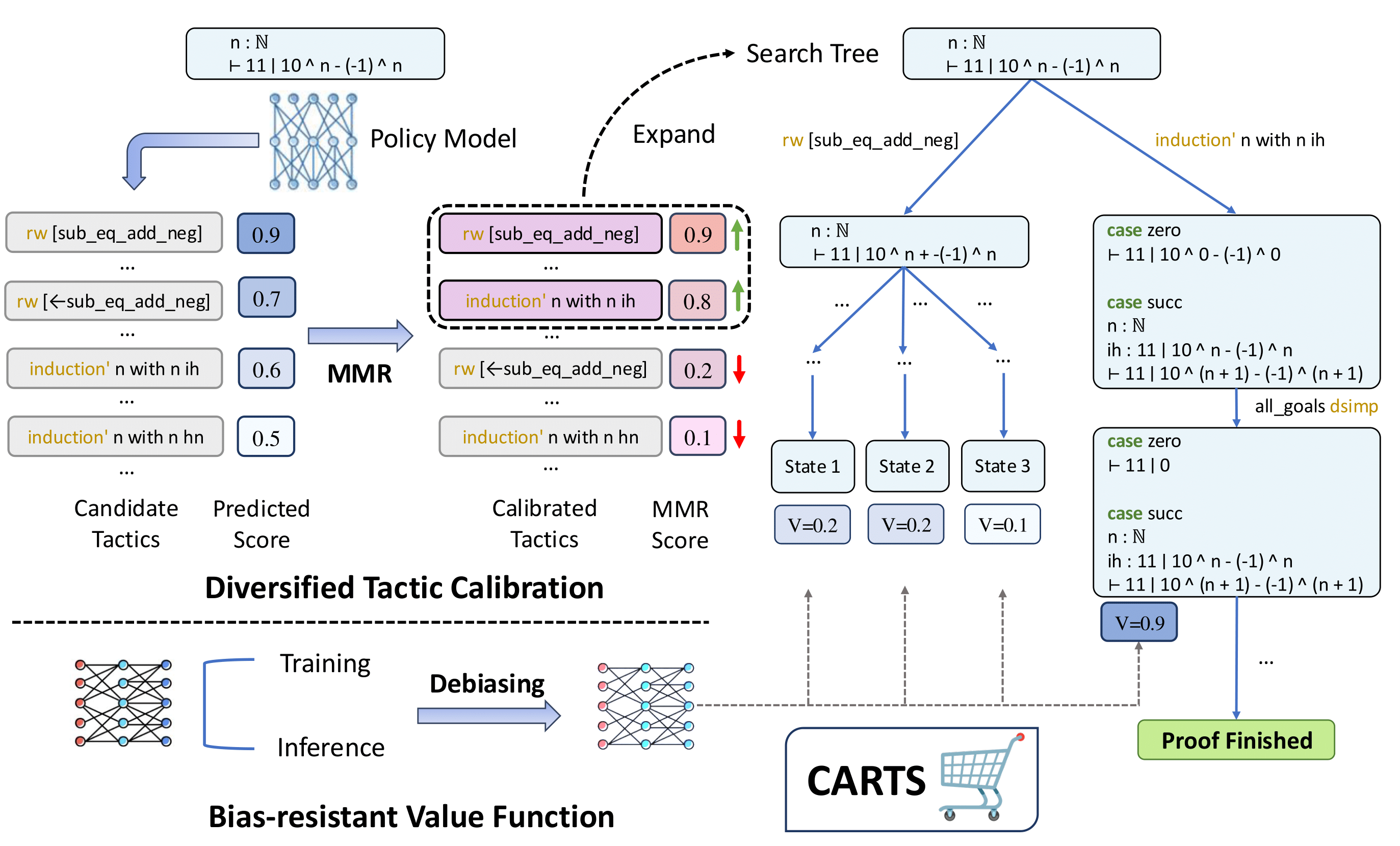
In theorem proving, language models often generate multiple candidate tactics that exhibit redundancy, which can hinder exploration. To address this, we introduce Diversified Tactic Calibration, which reorders tactics based on their importance (model confidence) and diversity. This is achieved using the Maximal Marginal Relevance (MMR) algorithm, integrated into a modified MCTS framework. The MCTS process in CARTS consists of three key steps:
The algorithm starts at the root node and traverses the tree to a leaf node, selecting actions that balance exploration and exploitation. The selection is guided by a Weighted Upper Confidence Bound (WUCB) score, which incorporates both the accumulated value of actions and a weight representing their importance and diversity. The WUCB score is calculated as:
\[ \text{WUCB}(s,a) = \frac{W(s,a)}{N(s,a)} + w(s,a) \cdot \frac{\sqrt{N(s,\cdot)}}{N(s,a)} \]
Here:
During this phase, the language model generates multiple candidate tactics, which are verified using the Lean 4. Verified tactics are then reordered using the MMR algorithm to ensure diversity and importance. The MMR score for each tactic \(a_i\) is calculated as:
\[ \text{MMR}(s,a_i) = \lambda \cdot v_{policy}(s,a_i) - (1 - \lambda) \cdot \max_{s_j' \in S} f_{enc}(s_i')^\top f_{enc}(s_j') \]
Where:
The MMR algorithm iteratively selects tactics that maximize this score, ensuring a diverse and high-quality set of tactics. These tactics are then expanded into the search tree, with their weights \(w(s,a_i)\) set to their MMR scores to encourage exploration of diverse tactics.
After expanding the tree, the algorithm updates the statistics of nodes and edges along the search trajectory. A bias-resistant value function \(V(s,a)\) is used to evaluate the value of actions, and this value is propagated back through the tree. Specifically:
This ensures that the search tree reflects the outcomes of simulations, improving future selections.
In MCTS-based methods, training a value function is crucial, typically involving the creation of positive and negative samples using the policy network on training data. Positive samples consist of correct actions (or trajectories) from the dataset, while negative samples are those generated by the policy network that lead to undesirable states. Binary cross-entropy loss is then used to train the value network.
Due to the hardness of verifying the correctness of actions not on the proof path, previous work often treats these actions as negative samples, resulting in an excessive number of negative samples, some of which are even inaccurate. This makes binary loss unsuitable and biases the value function. Furthermore, the domain gap between the training and test datasets also contributes to biases. In this paper, we conduct debiasing during both training and inference stages, as detailed below.
To mitigate bias introduced by data collection, we first structure the dataset into preference pairs of positive and negative samples. We utilize an embedding model \( f_{enc} \) to effectively filter out noisy samples. Specifically, if \( f_{enc}(s')^\top f_{enc}(s_{pos}') > \tau \), we discard the action \( a \). Here, \( s' \) is the next state from a sampled negative action \( a \) at the current state \( s \), \( s_{pos}' \) is the correct next state, and \( \tau \) is a threshold. This filtering ensures that the selected negative actions are more likely to be undesirable, thus reducing data noise.
Moreover, we adopt the preference modeling framework to train our bias-resistant value function. We employ the Bradley-Terry (BT) model, a widely used technique for preference modeling. The BT model posits that the probability of action \(a_{pos}\) being preferred over action \(a_{neg}\) given state \(s\) is expressed as: \[ \mathbb{P}(a_{pos} \succ a_{neg} \mid s) = \frac{\exp(V_\theta(s,a_{pos}))}{\exp(V_\theta(s,a_{pos})) + \exp(V_\theta(s,a_{neg}))} \] Assuming access to the filtered dataset \(D=\{(s^{(i)},a_{pos}^{(i)},a_{neg}^{(i)})\}_{i=1}^{N}\), we can parametrize the value function \(V_{\theta}(s, a)\) and estimate the parameters \(\theta\) by minimizing the negative log-likelihood.
Preference modeling offers several advantages. Firstly, by only providing the relative superiority among samples, false negative samples do not require further processing. This is because we can reasonably assume that the correct proof steps provided in the dataset are always optimal and align with human theorem proving's preferences. Additionally, since the dataset is presented in the form of preference pairs, this effectively oversamples the positive pairs, alleviating the issue of class imbalance between positive and negative samples, as demonstrated in some studies.
To mitigate the domain gap between the training and test datasets, we introduce an adjustment term into the value function during the inference stage. As previously mentioned, before calibration in CARTS, all \(E\) tactics should be processed through the Lean system to filter out \(e\) valid tactics. Intuitively, if the number of valid tactics is small, people will raise concerns about the capability of the current policy model, needing for a reduced reward for the current action. We define this reward adjustment as: \( \alpha = e/E \), representing the ratio between the number of valid tactics and the total number of tactics generated by the language model at the current state. This adjustment term serves as a test-time adaptation to the test dataset. The final bias-resistant value function integrates both the trained value network and this adjustment term as: \[ V(s, a) = \begin{cases} 0, & \text{if } s' \text{ has no child nodes,} \\ 1, & \text{else if } s' \text{ is the proved state,}\\ \frac{1}{2}(\alpha + V_\theta(s, a)), &\text{otherwise.} \end{cases} \] Where \(s'\) is the next state.
Unlike the intrinsic reward introduced by DeepSeek-Prover-V1.5, which only considers whether the search expands nodes, we consider both the expansion capability of the policy network and the generalizability of the value network, forming our final bias-resistant value function. The adjustment term can be interpreted as a form of test-time adaptation to the distribution of test data, thus can mitigate the domain gap.
We conduct experiments on MiniF2F and ProofNet.
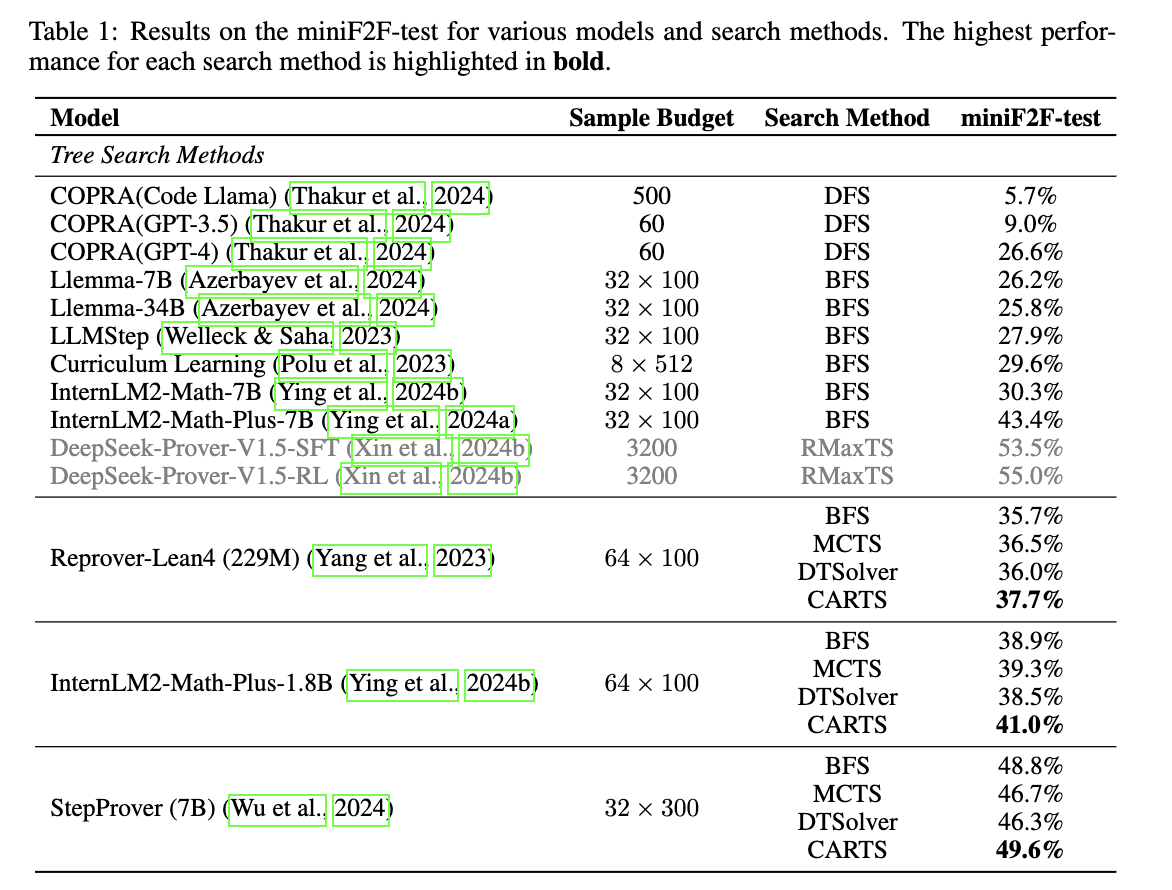
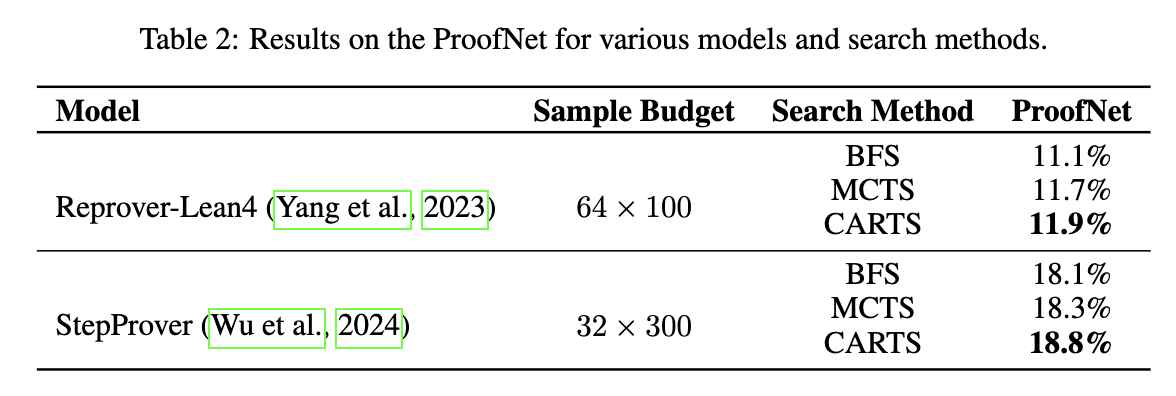
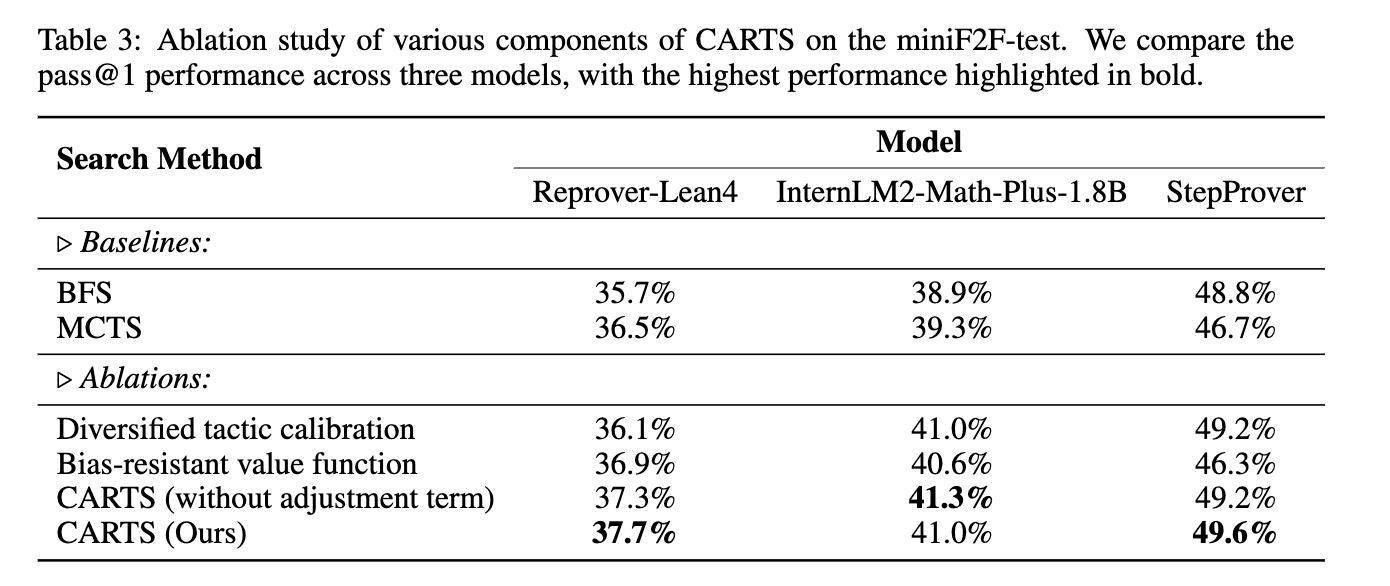
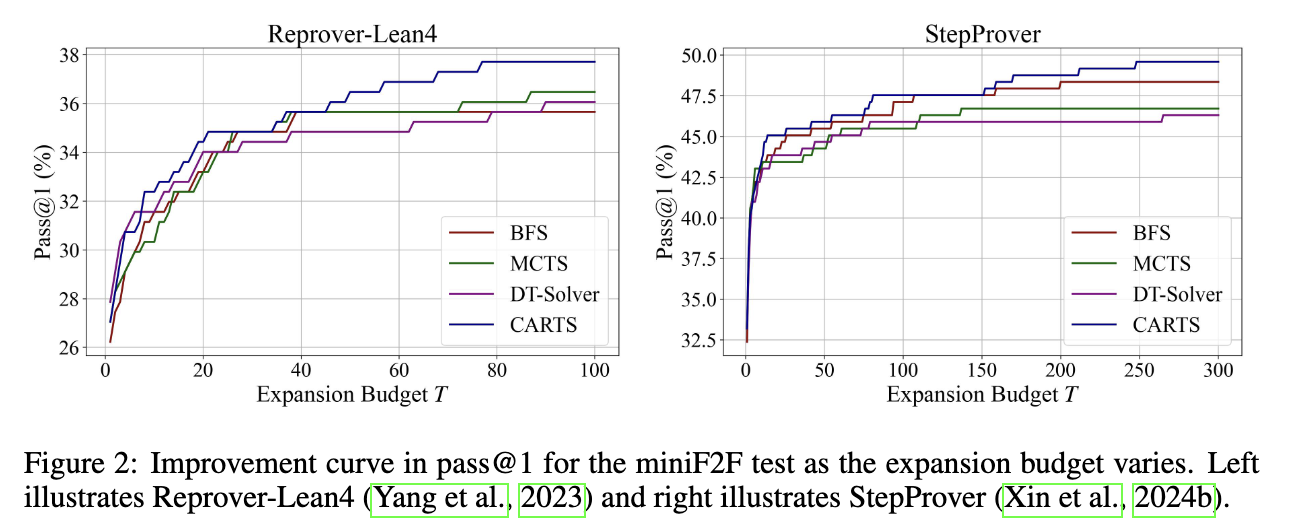
We also do some analysis. More results can been found in the paper.
@article{carts2025,
title={CARTS: Advancing Neural Theorem Proving with Diversified Tactic Calibration and Bias-Resistant Tree Search},
author={Yang, Xiao-Wen and Zhou, Zhi and Wang, Haiming and Li, Aoxue and Wei, Wen-Da and Jin, Hui and Li, Zhenguo and Li, Yu-Feng},
journal={ICLR},
year={2025}
}