Analysis for Abductive Learning and Neural-Symbolic Reasoning Shortcuts

Xiao-Wen Yang, Wen-Da Wei, Jie-Jing Shao, Yu-Feng Li, Zhi-Hua Zhou

Neural-symbolic learning (NeSy) and abductive learning (ABL) have been demonstrated to be effective by enabling us to infer labels that are consistent with prior knowledge. However, their generalization ability is influenced by reasoning shortcuts, where high accuracy is attained by exploiting unintended semantics. This paper conducts a theoretical analysis to quantify and alleviate the harm caused by reasoning shortcuts.

Reasoning Shortcuts in Neural-Symbolic Systems

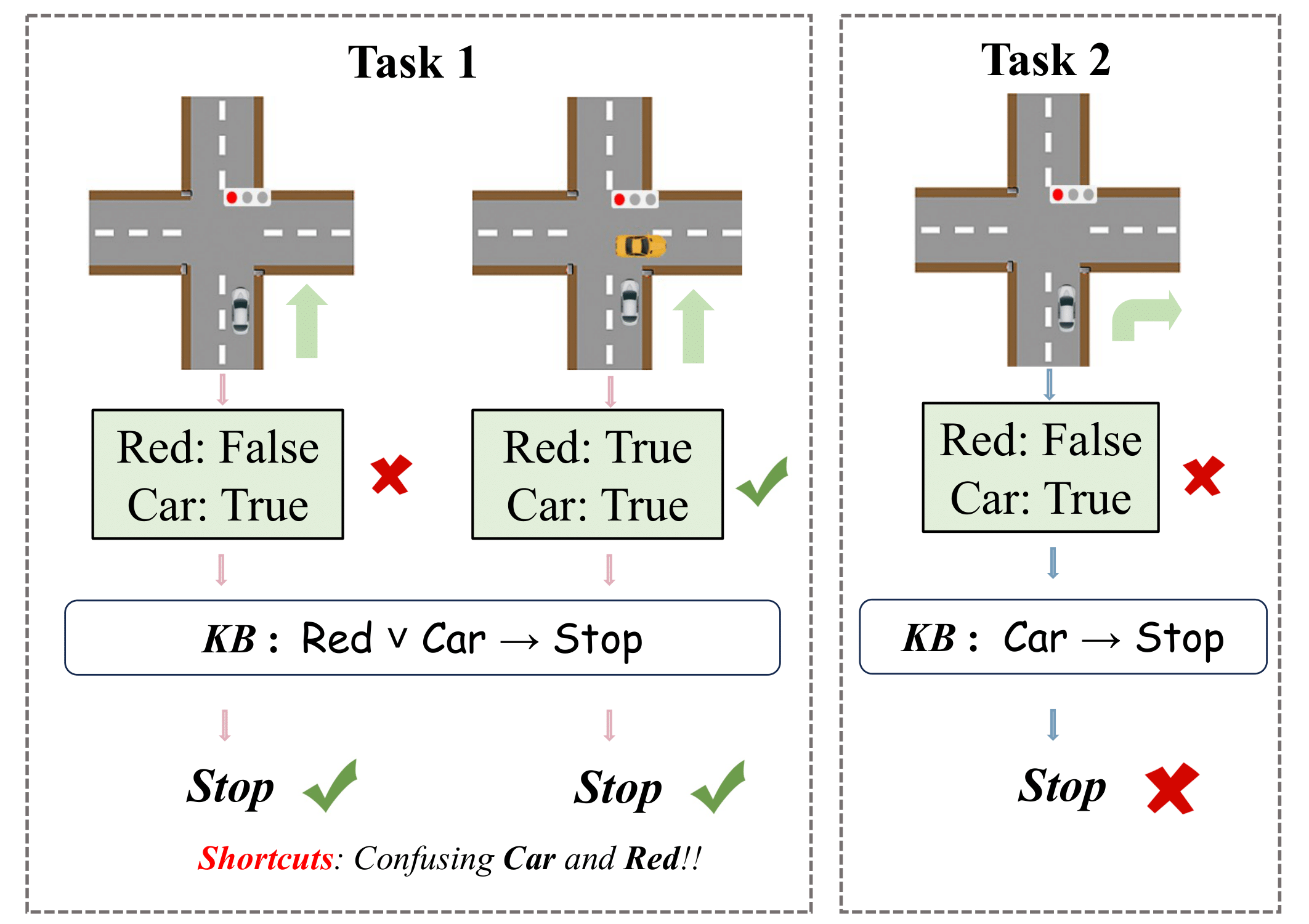
Reasoning shortcuts occur when neural networks acquire inaccurate semantics due to the absence of grounding labels for intermediate concepts. This leads to high performance on training tasks but poor generalization to new tasks. For example, in the figure above, an autonomous vehicle needs to decide whether to move forward or stop based on the given rule in Task 1: Red ∨ Car → Stop, which means it should stop whether there is a red light or a vehicle ahead. The model trained on this task could correctly classify the target, but it acquires a reasoning shortcut by confusing the presence of a vehicle and the red light. When the perception model learned in Task 1 is applied to Task 2, which involves determining whether turning right is permissible, the autonomous vehicle mistakenly decides it should stop when the perception model incorrectly predicts a vehicle ahead, possibly resulting in a dangerous situation.

Quantify Harm of Reasoning Shortcuts

Shortcut Risk

Many researchers pointed out that the optimization of representative neural-symbolic algorithms such as DeepProblog, LTN, and Semantic Loss can have a general form, that is given a training dataset S, find f ∈ 𝓕 that minimizes:

$Neural-Symbolic Loss Function$

In light of the fact that the incorrect intermediate concept satisfying the symbolic knowledge may also occupy a term within the loss function, this objective does not sufficiently guarantee the correct prediction of intermediate symbolic concepts, thereby giving rise to the issue of reasoning shortcuts.

Considering a supervised learning task whose target is to directly learn f given grounding labels of intermediate concepts. The objective of this task is to minimize the cross-entropy loss 𝓛 under the joint distribution of $(\mathbf{x}, \mathbf{z}, \mathbf{y})$ , i.e.,

$Cross-Entropy Loss$

We believe that if f can minimize 𝓛, then there would be no occurrence of shortcut problems. However, in real neural-symbolic tasks, we do not optimize along the same objective but optimize $\hat{\mathcal{L}}_{nesy}$ using a training dataset of limited size. This leads to the emergence of the reasoning shortcut problem. Hence, we define the severity of reasoning shortcuts as the disparity between our desired objectives and the attainable objectives within a finite dataset. Formally, the shortcut risk $R_s$ is defined as:

$Shortcut Risk$

The shortcut risk represents the severity of the reasoning shortcuts. The larger $R_s$ , the more severe the issue of reasoning shortcuts.

Knowledge Base Complexity

The complexity of the symbolic knowledge base (KB) is a key factor influencing the severity of reasoning shortcuts. It depends on data dependence and rule dependence, which affect how the knowledge base contributes to the neural-symbolic system. High complexity reduces the likelihood of reasoning shortcuts. The complexity of KB, denoted as $D_{KB}$ , is defined as:

$Definition of KB Complexity$

$D_{KB}$ is defined as the expected count of instances $\mathbf{z}$ that conflict with the knowledge base. Intuitively, if the complexity of KB is sufficiently high, it is more likely to encounter contradictions with $\mathbf{z}$ , thus resulting in a large $D_{KB}$ .

Main Results

About NeSy

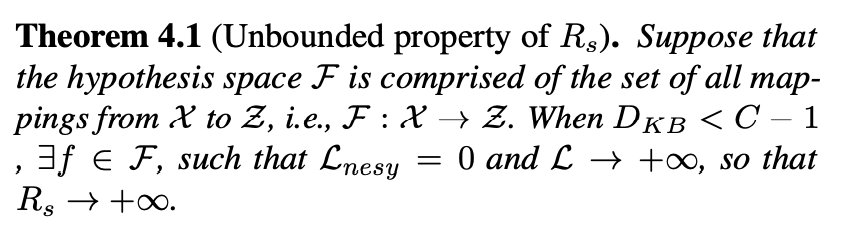
Theorem 4.1 showcases the unbounded nature of $R_s$ when the hypothesis space $\mathcal{F}$ exhibits sufficient complexity but the complexity of the knowledge base is insufficient. In such cases, the learned function $f$ satisfies the knowledge base for all training samples, thus $\mathcal{\hat{L}}_{nesy}=0$ . Simultaneously, it produces erroneous predictions for the intermediate concept $\mathbf{z}$ across all samples, leading to the desired objective loss $\mathcal{L}$ towards infinity. Consequently, the absence of constraints on the hypothesis space $\mathcal{F}$ greatly increases the risk of reasoning shortcuts.

Then in Theroem 4.5, we show that the shortcut risk has an upper bound when we restrict the hypothesis space. $R_s$ can be bounded by three terms. The first term relates to the complexity of the knowledge base, where a more complex $\mbox{KB}$ leads to a tighter upper bound for $R_s$ . The second term corresponds to the convergence of the number of training samples, following a rate of $\mathcal{O}(1/\sqrt{N})$ . The third term comprises the empirical Rademacher complexity of the hypothesis space and a constant factor, which characterizes the properties inherent to the hypothesis space itself.

About ABL

We analyze the reasoning shortcut problem of the ABL framework. We prove that the shortcut risk of the ABL algorithm, denoted as $R_s^{ABL}$ , is consistently smaller than that of the NeSy algorithm, and if we can construct a reasonable distance function, $R_s^{ABL}$ will have an upper bound of asymptotic rate $\mathcal{O}(\kappa)$ where $\kappa$ represents the error rate of the distance function. This means that the reasoning shortcuts may be greatly alleviated, showcasing its potential to address the shortcut problem. More details can be seen in the paper.

Experiments

We empirically corroborate two principal findings that have previously been supported by theoretical evidence: (1). As the complexity of the knowledge base increases, both the neural-symbolic approaches and the ABL algorithms exhibit lower shortcut risk. (2). The selection of the distance function Dis influences the performance of the ABL algorithm significantly, where a good choice of Dis can assist in alleviating the reasoning shortcuts.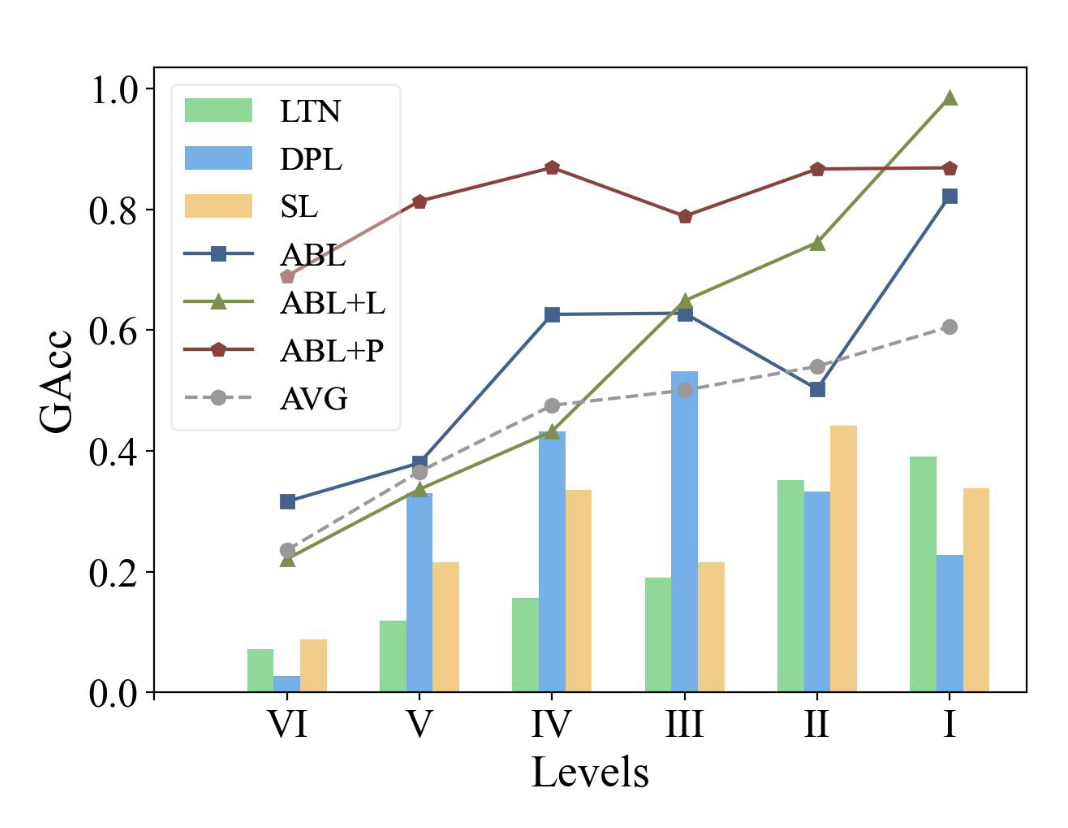

BibTeX

@inproceedings{yangshortcut,
  title={Analysis for Abductive Learning and Neural-symbolic Reasoning Shortcuts},
  author={Xiao-Wen Yang and Wen-Da Wei and Jie-Jing Shao and Yu-Feng Li and Zhi-Hua Zhou},
  booktitle={Proceedings of the International Conference on Machine Learning},
  year={2024},
}

Xiao-Wen Yang (杨骁文)